Master Machine Learning Algorithms 一书第2章节内容翻译。

数据在机器学习中起着重要的作用。在讨论数据时，理解和使用正确的术语是非常重要的。在本章节中你会发现如何在机器学习中描述和讨论数据。阅读本章后，你会知道：

在讨论数据电子表格时，一般使用标准的数据术语
统计中使用的数据术语和机器学习的统计视图
在机器学习的计算机科学角度中使用的数据术语

这将大大帮助你理解一般的机器学习算法。

如你所知的数据

你如何看待数据？想一下电子表格，其中有列、行和单元格。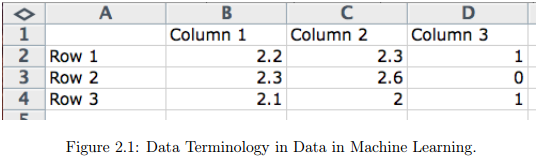

列：列描述的是单个类型的数据。例如，你可以有一列重量、高度和价格。一列中的所有数据具有相同的比例，并且拥有相对于彼此的含义。
行：行描述的是单个实体，列则是实体的属性。你拥有的行越多，则拥有的问题域中的样例越多。
单元格：单元格是行和列的单个值。它可能是一个实数值（1.5）、一个整数值（2）或一个类别（red）。

这就是你可能会考虑的数据，列，行和单元格。通常，我们可以称这种类型的数据为表格数据（tabular data）。这种格式的数据很容易在机器学习中应用。机器学习有不同的风格，可以在这个领域上带来不同的视角。例如，有统计学角度和计算机科学角度。接下来我们将看到不同的指代数据的术语。

统计学习角度

在统计学角度中，是在机器学习算法试图学习的假想函数（f）的环境下，构建数据。也就是说，给定一些输入变量（输入），预测的输出变量（输出）为：
$$Output = f(Input)$$
那些作为输入的列被称为输入变量。那些你可能并不总有的数据列，且在将来想要为新输入数据预测的数据称为输出变量，也称为响应变量。
$$OutputVariable = f(InputVariables)$$

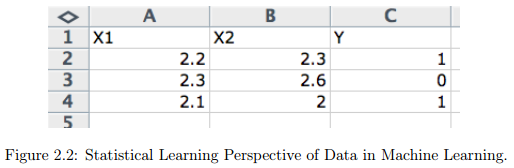
通常，你有多个输入变量。在这种情况，输入变量组可称为输入向量。
$$OutputVariable = f(InputVector)$$
如果你在之前有学过一些统计方面的内容，你就会知道另一个更传统的术语。例如，统计学中一些文本可能会将输入变量称为独立变量，输出变量称为因变量。这是因为在预测问题中，输出依赖于输入或自变量（独立变量）的函数。
$$DependentVariable = f(IndependentVariables)$$

数据在等式和机器学习算法中均使用简短的描述。在统计学中标准速记法试讲输入变量记为大写的x（$X$），输出变量为大写的y（$Y$）。
$$Y = f(X)$$
当你有多个输入变量时，可以用一个整数来表明它们在输入向量中的索引位置，例如，X1、X2、X3，分别对应前三列。

计算机科学角度

从统计学的角度来看，数据在计算机科学术语中有很多重叠部分。我们可以来看下几个关键的区别。行通常描述的是一个实体（例如，一个人）或是对一个实体的观察。行中的列通常被称为观察的属性。当对一个问题进行建模和做出预测时，我们可能会参考输入属性和输出属性。
$$OutputAttribute = Program(InputAttributes)$$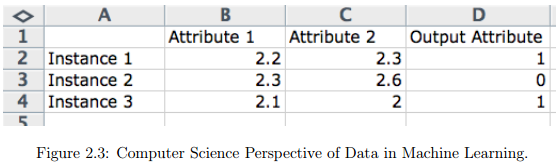

关于列的另一个名称则为特征，用于与属性相同的原因，其中一个特征描述的是观察的一些属性。在使用必须从原始数据中提取特征构建观察的数据时，这种情况更为常见。这方面的样例，包括模拟数据，例如，图像、音频和视频。
$$Output = Program(InputFeatures)$$
另一个计算机科学的措辞是将数据或观察的一行称为一个实例（instance）。这是因为一行可能被视为是由问题域观察或生成的单个样例或单个数据实例。
$$Prediction = Program(Instance)$$

模型和算法

最后有一个重要的说明需要强调下，那就是算法和模型的关系。这可能会令人很困惑，因为算法和模型可能互换使用。我喜欢的一个观点是，将模型视为从数据中学习得具体表示，将算法视为学习它的过程。
$$Model = Algorithm(Data)$$
例如，一个决策树或一组系数是一个模型，C5.0和最小二乘线性回归（Least Squares Linear Regression）是学习那些模型的算法。

总结

在本章中，你学到了在机器学习中用于描述数据的关键术语。
对表格数据有了标准理解，如列、行、单元格；
学习到了输入和输出变量的统计学术语，其分别表示为X和Y；
学习到了计算机科学术语：属性、特征和实例；
最后，学习到了可以将模型和算法分别看作是学习表示和学习过程。

现在你已经知道了如何在机器学习中讨论数据。接下来的章节中，你将会学到所有机器学习算法的基础范例。