这是本人在学习TensorFlow实战一书时所记录下来的一些内容。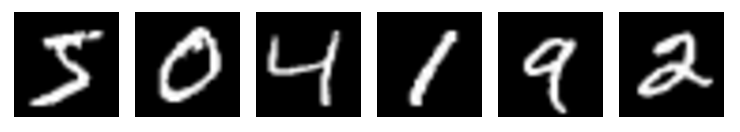

MNIST数据集

MNIST（Mixed National Institute of Standards and Technology database）是一个非常简单的机器视觉数据集，如上图所示，它由几万张28像素x28像素的手写数字图片组成，这些图片只包含灰度值信息（channel=1）。
我们所需要做的任务就是对这些手写数字的图片进行分类，转成0~9一共10类。

首先对MNIST数据进行加载，TensorFlow为我们提供了一个方便的封装，可以直接加载MNIST数据成我们期望的格式。
在Jupyter上运行代码：

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data", one_hot=True)
print(mnist.train.images.shape, mnist.train.labels.shape)  
print(mnist.test.images.shape, mnist.test.labels.shape)    
print(mnist.validation.images.shape, mnist.validation.labels.shape)

结果显示为：

Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.
Extracting MNIST_data\train-images-idx3-ubyte.gz
Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.
Extracting MNIST_data\train-labels-idx1-ubyte.gz
Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.
Extracting MNIST_data\t10k-images-idx3-ubyte.gz
Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.
Extracting MNIST_data\t10k-labels-idx1-ubyte.gz
(55000, 784) (55000, 10)
(10000, 784) (10000, 10)
(5000, 784) (5000, 10)

数据集成功下载获得，并打印出mnist的训练集中有55000张图像，784维的特征，测试集有10000张图像，验证集有5000张图像。

注：
1) 图像是28像素x28像素大小的灰度图片，即空白部分全部为0，有笔迹的地方根据颜色深浅有0到1之间的取值。
2) 每个样本有784维的特征，来自于将28x28个像素点展开成一维的结果（28x28=784）。
3) 此处简化了问题，丢弃图像的空间结构的信息，将图片按同样的顺序展开至1维向量即可。
4) 训练数据的特征是一个55000x784的Tensor，第一个维度是图片的编号，第二个维度是图片中像素点的编号。同时训练的数据Label是一个55000x10的Tensor。测试集、验证集同样道理。
5) 读取数据时，对10个种类进行了one-hot编码，Label是一个10维的向量，只有1个值为1，其余为0。比如数字0，对应的Label就是[1,0,0,0,0,0,0,0,0,0]，数字5对应的Label就是[0,0,0,0,0,1,0,0,0,0]，数字n就代表对应位置的值为1。

Softmax Regression

数据准备好后，我们采用的是一个叫Softmax Regression的算法来训练手写数字识别的分类模型。
数据集的数字都是0~9之间的，所以一共有10个类别。
当模型对一张图片进行预测时，Softmax Regression会对每一种类别估算一个概率，比如预测是数字3的概率为80%，是数字5的概率为5%，最后取概率最大的那个数字为模型的输出结果。

$i$代表第$i$类，$j$代表一张图片的第$j$个像素，$b_i$是bias。$$feature_i = \sum_j W_ix_j + b_i$$
接下来对所有特征计算Softmax，即计算一个exp函数，然后再进行标准化（让所有类别输出的概率值之和为1）。
$$softmax(x) = normalize(exp(x))$$
其中判定为第$i$类的概率可由下面公式得到：
$$softmax(x)_i = \frac{exp(x_i)}{\sum_jexp(x_j)}$$

整个Softmax Regression的流程如下图所示：
softmax
转换为公式的话，如下图所示，将元素相乘变成矩阵乘法：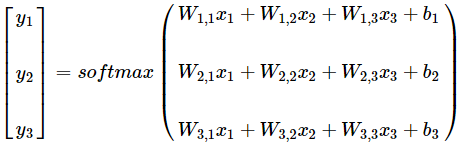
softmax
即：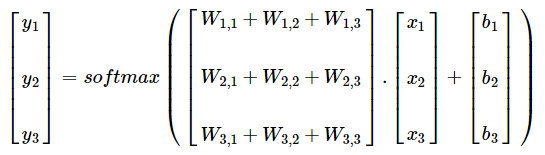
softmax
上述矩阵表达写成公式的话，就可用下面一行表达：
$$y = softmax(Wx + b)$$

TensorFlow实现

import tensorflow as tf
sess = tf.InteractiveSession()  # 将InteractiveSession注册为默认的session，之后的运算默认跑到这个session里
# 不同session之间的数据和运算都是相互独立的
x = tf.placeholder(tf.float32, [None, 784])  
# 创建placeholder，输入数据。第一个参数是数据类型，第二个参数是tensor的数据尺寸，这里None代表不限制条数的输入，784维向量

1 2	W = tf.Variable(tf.zeros([784, 10])) # Weights参数，Variable在模型训练迭代中式持久化的。weights初始化为0 b = tf.Variable(tf.zeros([10])) # bias全部初始化为0

注：
1) 存储数据的tensor一旦使用就会消失，但Variable在模型训练迭代中是持久化的，可长期存在并在每轮迭代中被更新。
2) 这里全部初始化为0，因为模型训练时会自动学习合适的值，对这个简单模型来说初始值不太重要。
3) 但对于复杂的卷积网络、循环网络或较深的全连接网络，初始化得方法比较重要。

1
2
3

# y = softmax(Wx + b) 改写成TensorFlow语言
y = tf.nn.softmax(tf.matmul(x, W) + b)  # 实现Softmax算法
# tf.matmul 矩阵乘法函数

y_ = tf.placeholder(tf.float32, [None, 10])  # 输入真实的label的概率分布 y_
# 损失函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))  
# reduce_sum求和的cgama， reduce_mean对每个batch数据结果求均值

注：
1) 损失函数越小，代表模型的分类结果与真实值的偏差越小，即模型越精确。
2) 训练的目的是不断将这个损失减小，直到达到一个全局最优或者局部最优解。
3) 对多分类问题，通常使用cross-entropy交叉信息熵来作为损失函数。

1
2
3

# 定义一个优化算法，设置学习率，设定优化目标为cross-entropy
# 常用 随机梯度下降SGD算法
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)  # 学习率0.5

1 2	# 使用TensorFlow的全局参数初始化器tf.global_variables_initializer，并直接运行run方法 tf.global_variables_initializer().run()

# 迭代训练操作train_step
# 每次随机从训练集中抽取100条样本构成一个mini-batch，并feed给placeholder，调用train_step进行训练
for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    train_step.run({x: batch_xs, y_:batch_ys})

1	correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))

注：argmax获取的是最大值所在位置索引，所以一个是y中概率最大的那类所在位置索引，另一个是真实值y_中最大（即值为1）的位置索引，之后将两者进行equal比较，相等则为true，反之false，最后获得correct_prediction的bool矩阵。

# 统计全部样本预测的accuracy，先用cast将之前的correct_prediction输出的bool值转换为float32，再求平均
# bool转float，即true为 1.0，false为 0.0
# 用reduce_mean计算平均值，即为精度值：相等（1.0，即预测正确）的数量在总数量中的占比
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

1 2	# 将测试数据的特征和label输入评测流程accuracy，计算模型在测试集上的准确率 print(accuracy.eval({x: mnist.test.images, y_: mnist.test.labels}))

最后的预测精度约为92% 。

附上程序：https://github.com/asdfv1929/TensorFlowInActionLearning (TensorFlow实现Softmax Regression识别手写数字)